近日，叶芳伟课题组在无序系统中波的演化这一前沿科学问题上取得突破。课题组的秦建伟（第一作者）、刘岩（共同第一作者）与叶芳伟（通讯作者）通过理论模型、数值模拟与实验验证，首次系统地揭示了光波在时间上涨落的随机势场中演化时，会经历从分支流到安德森局域化的过渡过程，并精准预测了其中的两个关键临界点。相关研究成果已于近期发表于学术期刊Laser & Photonics Reviews。

背景：无序世界中的两种普遍波现象

波在不同的无序介质中传播时，其命运可能截然不同。在静态无序系统中，会出现著名的安德森局域：波因多次散射产生的相干相消而被完全囚禁在空间一隅。这一现象是凝聚态物理和波动物理的基石之一。相反，在含时变化的动态无序系统中，波会展现出奇妙的分支流现象：波前会自发汇聚成无数条明亮、稳定的分支通道，如同闪电或河流，在介质中持续延伸和分叉，展现出远超常规的扩散能力。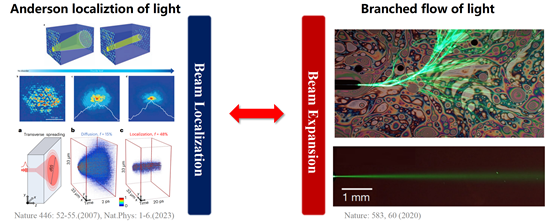

图1，光的安德森局域（左）与分支流（右）。

长期以来，这两种现象——安德森局域网和分支流——被视为分别对应于静态与动态无序系统的两种独立范式。一个核心的问题是：如果无序势场的演化速度由快变慢，波的传播行为将如何连续地从一个极端（分支流）过渡到另一个极端（安德森局域化）？

研究创新：引入“时间关联长度”作为调控旋钮

为解决这一问题，课题组引入了一个关键调控参数——时间关联长度（τ），它描述了随机势场在演化方向（如光传播方向或时间维度）上保持相关的长度尺度。τ 越小，势场变化越快；τ越大，势场变化越慢；当 τ 趋于无穷大时，势场退化为静态。研究团队通过求解无量纲薛定谔方程，系统模拟了高斯波包在不同 τ 值的随机势场中的演化，并以均方位移（MSD）和扩散指数(γ)作为定量判据，以区分不同的波动范式。

核心发现：非单调的扩散过渡与三个鲜明的区域

研究发现，波的扩散行为并非随 τ 增加而单调变化，而是呈现出丰富的物理图像。

1.  分支流主导的超扩散区：当 τ 较小时，势场的快速涨落抑制了相干局域化，分支流效应显著。波的扩散速率（γ）随 τ 增加而提升，甚至超过弹道扩散（γ=2），达到理查森型超扩散（γ≈3），即扩散速率达到峰值。

2.  相干局域化崛起的竞争区：当 τ 超过第一个临界值后，部分波模式开始“感知”到势场的缓慢变化，其相干性得以维持。安德森局域化效应开始显现，与分支流效应竞争，导致整体扩散速率 γ 随 τ 增加不升反降。

3.  安德森局域化主导的完全局域区：当 τ 超过第二个更大的临界值后，所有波模式都能在其特征时间内保持稳定的相干性。此时，波被完全局域在初始位置附近，扩散指数 γ 降至零，实现了动态无序下的准安德森局域化。

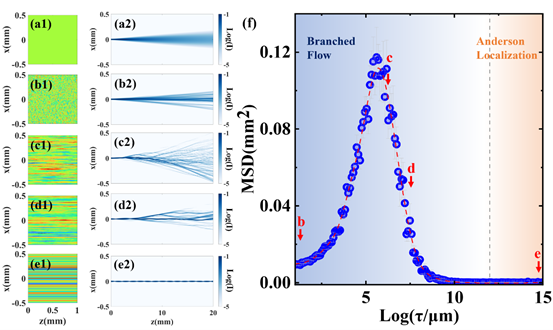
图2 高斯波包在不同时间关联长度τ下的扩散行为以及MSD与τ的非单调关系。可以看到，随着τ的增加，波从一开始的扩散（第一行），变成分支流（第二、第三行，此时波扩散得更剧烈），最后过渡到分支流-安德森竞争区（第四行，此时波扩散减弱），乃至最终收敛到常规的安德森局域（第五行）。

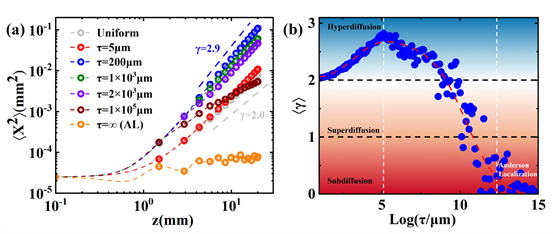
图3 （a）不同时间关联长度τ下，MSD与演化距离的关系 （b）不同关联长度下，波包的扩散系数γ

为解释上述现象，课题组提出了一个简洁而深刻的有效势阱模型，较为精确地预言了临两个临界τ值。

波包演化从分支流过渡到安德森局域的情况，也在更高维度的系统中发生，如图4所示。

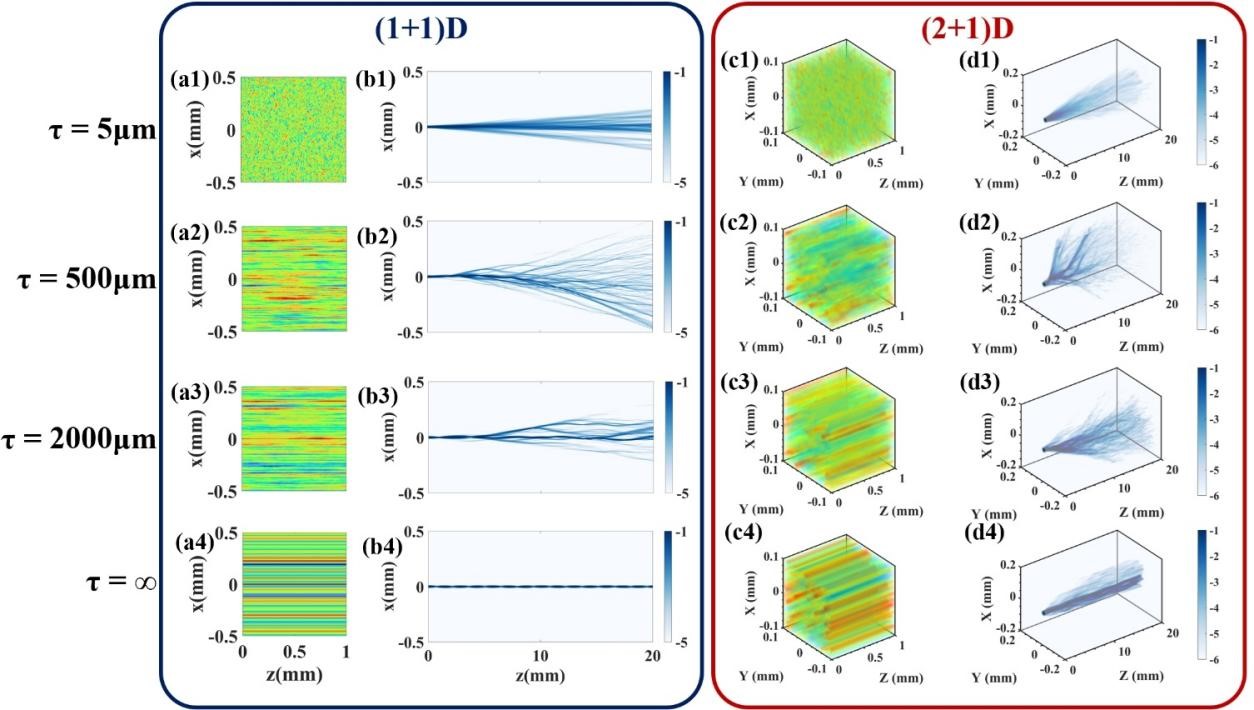
图4 （1+1）D（左）和（2+1）D（右）模拟中，高斯波包在不同时间关联长度τ随机介质中的演化。

 实验验证：光在光折变晶体中验证理论预言

课题组在光折变晶体SBN:61中，利用光学诱导技术，成功制备了具有极高各向异性（空间与时间关联长度之比达1:150）的(1+1)维无序势场。通过精确调控写入光场的纵向关联长度（即 τ），实验上清晰地观测到探测光束从强烈分支、超扩散到扩散被抑制、最终趋于局域化的整个过渡过程。实验测得的MSD 随 τ 的变化曲线，验证了数值模拟和理论预测的非单调行为。

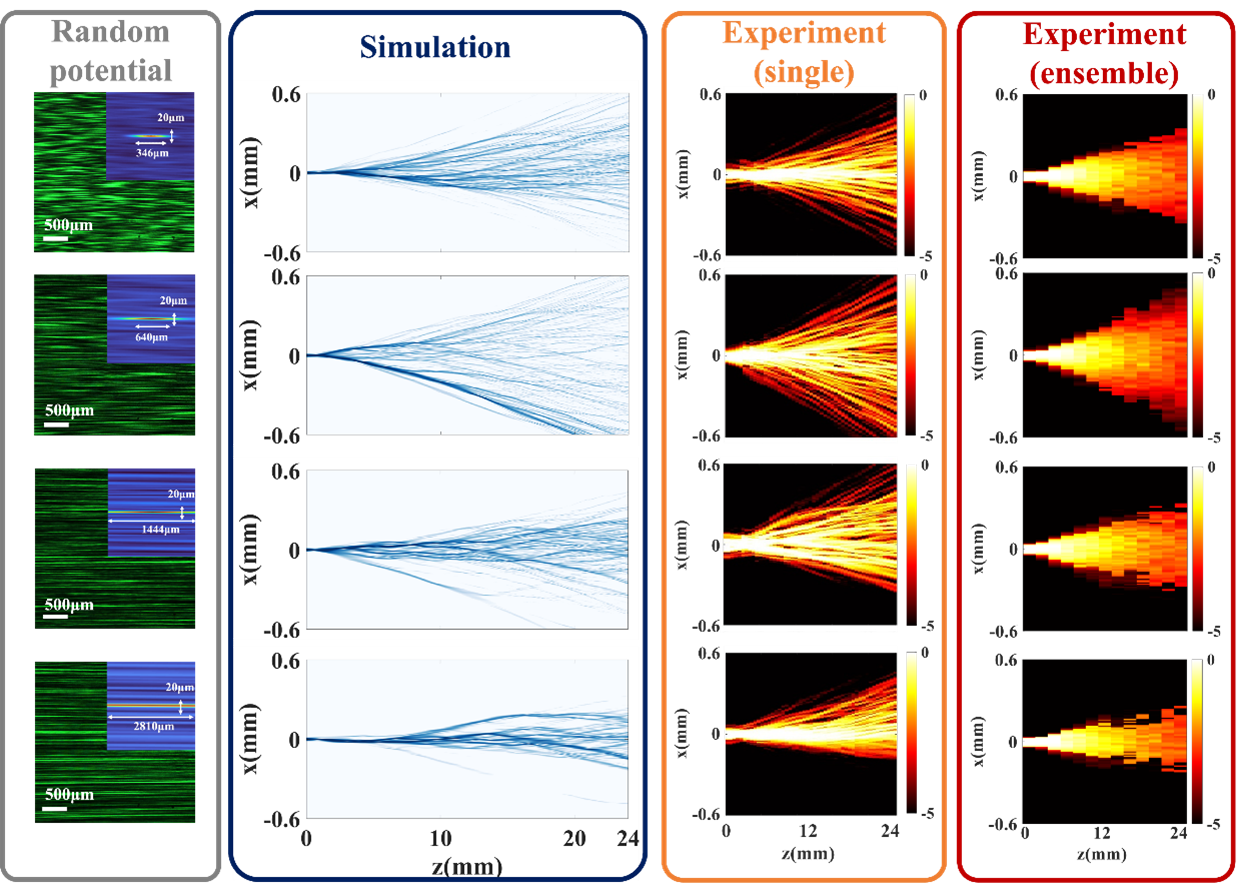
图5 在SBN晶体中，写入不同关联长度的随机折射率分布，以及光波在随机介质中的演化行为。

意义与展望 

该项研究首次完整描绘了在动态无序系统中，波的演化从扩散到局域的连续变化，统一了分支流与安德森局域化这两种看似矛盾的现象。除了光波，类似的转变过程在其他波动系统也有望被观察到，如声波、二维电子气、微波、表面波等。其揭示的物理规律具有普适性。

文章链接：http://doi.org/10.1002/lpor.202501144